Rechnen mit dem Bayes-Theorem
Technische Hintergründe zum M7 Coprozessor: So erkennt das iPhone 5s Schritte & Co.
Wie genau funktioniert die Aktivitätserkennung des im iPhone 5s verbauten M7 Coprozessors? Auf welche Schnittstellen können Entwickler, die an den vom iPhone 5s gesammelten Bewegungsdaten interessiert sind, setzen? Wie unterscheidet das iPhone die per Fuß zurückgelegten Strecken von denen, die als Autofahrten und Ruhephasen erkannt werden?
Der Motionprozessor ist durch die zahlreichen App Store-Neuveröffentlichungen der vergangenen Tagen in aller Munde; zu den Hintergründen des stromsparenden Logikbausteins, der es wohl auch in Apples iWatch schaffen wird, ist außerhalb der Entwickler-Community jedoch nur wenig bekannt.
Vorhang auf für Paul Balzer. Der Mitarbeiter des dresdner Unternehmens MechLab Engineering, beschreibt in seinem Artikel „Aktivitätenerkennung“ die Unterschiede der vom M7 ausgegebenen Status-Meldungen (stationary, running, walking, automotive und unknown) erklärt das Confidence-Rating, mit dem das iPhone die Sicherheit ermittelt, mit der die festgestellte Art der Bewegung wahrscheinlich zutrifft und gibt einen Einblick in die Welt der Algorithmen zur Aktivitätenklassifizierung, mit Hilfe sich die M7-Daten weiter verarbeiten lassen.
Wie also handhaben iPhone-Entwickler die Kommunikation ihrer Apps mit dem neuen iPhone-Chip am besten?
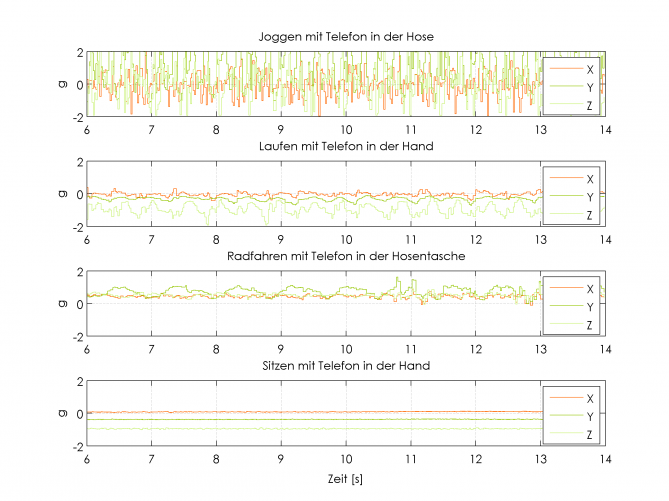
[…] Allein mit Hilfe der Drehrate und Beschleunigung ist es relativ einfach möglich, grundlegende Aktivitäten zu unterscheiden. Der hier aufgezeichnete und betrachtete Zeitraum war nur 8 Sekunden. Mit den Ergebnissen aus jeweils einer Periode kann eine Wahrscheinlichkeit berechnet werden, welche Aktivität gerade vorliegt. Z.B. könnte aus der Analyse der Signale berechnet werden, dass gerade Fahrrad gefahren wird.
Kommt der Algorithmus zu dem Ergebnis “radfahren”, so wird die Wahrscheinlichkeit, dass gerade wirklich Rad gefahren wird, erhöht. So kann über das Bayes’-Theorem mit vorhandener Wahrscheinlichkeit und neuer Erkenntnis eine “confidence” berechnet und ausgegeben werden. Zusätzlich können Zustandsübergänge als Markoff Ketten mit Wahrscheinlichkeiten bestimmt werden. Ein Übergang von joggen zu laufen ist wahrscheinlicher, als ein Übergang von joggen zu radfahren.

simpelste stochastik, bei der sich jeder börsen futzi langweilt. wie wärs mal mit einem theorem zur apple aktie. wenns funktioniert, machen wir gern eine theorie draus :D
das tracking wäre bei einer uhr sinnvoller. die trägt man stets bei sich. somit wäre es dann wohl auch möglich festzustellen, wie oft man am tag stuhlgang hat. das rockt ;D
Wirklich ne coole Sache, auch wenn sie jetzt nicht so viel praktischen Nutzen hat… Zumindest seh ich den nicht. Aber cool allemahl
Na, ist doch einfach da den Nutzen zu erkennen: Wenn Deine Bewegungs-Kurven eher so aussehen wie die oberen drei statt wie die unterste, obwohl Du sitzt, hast Du mit größter Wahrscheinlichkeit Parkinson. Insofern wird das 5s inzwischen z.B. unabdingbar für die klinische Diagnose-Praxis…
Grundlegend handelt es sich also um Näherungswerte an Referenzwerte. Das Prinzip ist an sich ja nichts neues. Die Methodik wird oft angewandt, zum Glück nun auch endlich im Telefon
Der Rest wurde vergessen: mir wäre ja ein vernünftiger Sleep-Tracker lieber, als eine App, die mir nach dem Joggen bestätigt, dass ich wirklich joggen war ;)
There is an App for that… ;-)
Auch eine, die den neuen m7 vollständig ausnutzt?
Warum willst du wissen wie du geschlafen hast?
Probiere es mit dem Sleep Time von Azurios Inc. Ich bin begeistert von dem Ding
Sleep Cycle ;-) …da werden Sie geholfen
Besser eine App., die Dir nach dem Schlafen bestätigt, dass Du geschlafen hast?
simpelste stochastik, bei der jeder börsen futzi gelangweilt gähnt :) bei ner uhr wäre das sinnvoller, die trägt man konstant. iwatch ich komme. obwohl, dann könnte man auch meinen stuhlgang tracken… wers mag :D
mir gehen diese angeberischen eingebildedetn börsenfuzis auf den sack was sie können hat man bei den rating-agrnturen gesehen. nichts
Ray, du scheinst oft „Stuhlgang“ zu haben….du solltest mal zum Onkel Doktor… ;-)
DRESDEN, wuhu :D
LIKE
Nachdem es offensichtlich ein paar Leute interessiert, habe ich noch ein Video hinzugefügt, welches das Markov Model ausführlich erläutert.